Learning the Number Facts Made Easy

Learning the Number Facts made easy…

I don’t call them ‘tables’, because I want children to see the connection between x, +, - and ÷

First of all, we need to understand that when we change the order in multiplication, the answer remains the same.

eg: 5 x 3 = 15 6 x 8 = 48

3 x 5 = 15 8 x 6 = 48

We don’t really need to practice the ones we know, just the ones we don’t know so well.

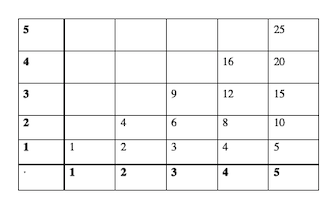
This is what it looks like. There are 100 number facts here, but each is listed twice.

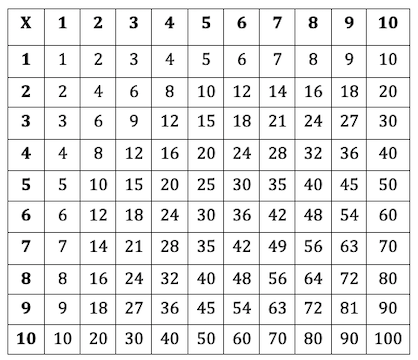
So, let’s get rid of the double ups…

Immediately we have cleared away half of them.

What do you notice about the highest number in each unhighlighted column?

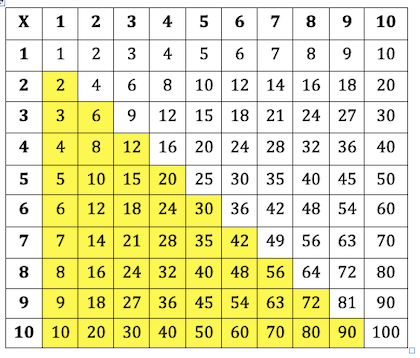
Now lets get rid of the number facts that we really know…

You have to be the judge of this.

Only highlight them if you are really sure that you know them.

1 x, 2 x, 5 x, 10 x

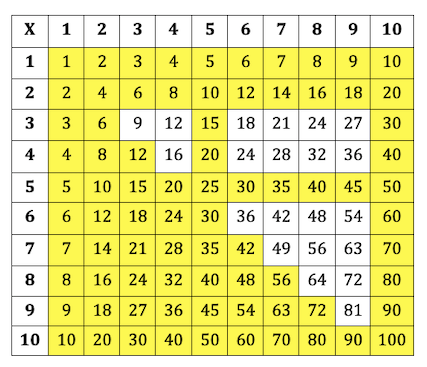
Perhaps you know your ‘Square Numbers’ really well too!! Eg 2 x 2, 3 x 3, 4 x 4 etc

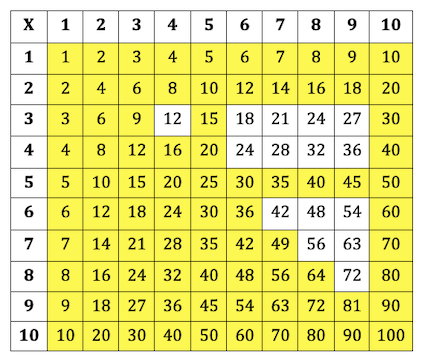
You might know some of these too, but it shows that there really aren’t a lot to learn.

Now we can focus on learning the more troublesome ones, and you might find that the list isn’t as large as first thought!

The important thing that I must stress is that we must understand the ‘turnaround process’, that 5 x 3 gives the same answer as 3 x 5.

When you say this problem, say it both ways so that the children see it as the same.

Make an array (rows and columns) that has 5 rows of 3. Now turn it around and highlight 3 rows of 5. The quantity remains the same!!

Now that we have identified what we need to learn, how about some strategies for doing this?

Often, we know what we need to learn, but can be unsure as to how to do it.

This could be particularly useful for parents at home with their children over the next few weeks.

Strategies for Learning Multiplication Facts

The usual approach to learning multiplication facts is to learn to chant through the multiplication facts in order.

Children learn the two times ‘table’, the three times ‘table’, then the four times ‘table’, then the fives, etc.

While we do need to memorise the basic multiplication facts, learning them by chanting them or by rote is not always the most helpful approach.

I’m keeping in mind here that many parents and teachers will disagree with this as “That’s the way that I was taught and I know them, so why do we do it this way?” I hear this constantly.

• Many children who have learned their ‘tables’ in this way can have difficulty remembering the facts without chanting through the table. The development of instant recall can be hindered rather than helping it.

• By setting out the multiplication facts in columns and learning each set of tables separately does not develop the commutative property ( eg turnaround facts). This means that many children who do know, 4 x 3 but do not relate it to 3 x 4 have to remember almost twice as many facts as they need to.

• Also, when they cannot recognise patterns like 4 times is double 2 times it increases the memory load for students.

By learning the facts in clusters, rather than all 100 together it can be easier for them to retain them.

Here’s an approach…

Build up the facts to 5 x 5 - rather than chanting through 10 columns.

Start with the twos (doubles), fours (double doubles), fives (because of the easy patterns and the links to our fingers) and then the threes. Put these in a two-way table. Commutativity ( or turnaround facts)reduces the 25 facts to be remembered to only 15, andif we remove the ones, there are only ten to remember.

Use the five by five table to show your children that by learning just ten facts they ‘get’ 25!

Practice these facts and build recall with frequent short periods of practice. Rather than working on 100 facts, the memory load is focusing on just 15!!

Often you will find that your children might skip count by 2, 3 or 5 to solve a question, but this still asks them to skip through the column of facts. This reduces their ability to develop instant recall, which hopefully will happen when we focus on a reduced number to start with.

The ones and twos

Focus on their ability to double a number. You will find that children will learn the ‘doubles’ before many other facts.

The tens

From the early years at school, the children become familiar by counting by tens. It’s important to apply the turnaround facts here so that children see that 3 x 10 and 10 x 3 are the same.

The squares

These are the ones that children often learn quickly as they create a strong visual on the chart (the diagonal line) and can also be a fun exploration. They can make a square with tiles for each of these. Because of this we find that they are often retained before others.

At this stage we have now covered the facts involving 1 x 1 to 5 x 5.

Also the facts for 1, 2, 10 and the square numbers. As you shade these in on your grid you will begin to see how many they actually do know already.

The remaining ‘facts’ can be developed in a number of ways.

You might find it helpful to move out in an ever-increasing square, so that the next cluster of facts is those to fill in the square to 6 x 6. This requires the addition of three new facts (6 x 3, 6 x 4, 6 x 5) and their ‘partner’ facts (3 x 6, 4 x 6, 5 x 6). Then move out to 7 x 7 and so on.

The five facts

Build up the five facts to 5 x 10, noting the relationship to the ten facts (e.g. five eights is half of ten eights; half of eight tens is four tens or 40; so 5 x 8 is 40) and the pattern in the units digits. Add to the table and memorise.

The four facts and eight facts to 8 x 8

First build on the ‘doubles’ or twos (2 x 1 to 2 x 10) to get the ‘double doubles’ or fours (to 4 x 10). Add these to the table.

Double the four facts to produce the eights up to 8 x 5 (if you know 4 x 3, you can double to get 8 x 3). Add these to the table.

Use commutativity/turnarounds to work out the extra facts (if you know 8 x 3 you also know 3 x 8).

When first practising these facts, give the children plenty of time to work them out mentally using the doubling strategy or some other method they prefer. Gradually build up speed to get ‘instant recall’. Use various doubling and other patterns to build up the extra eight facts (8 x 6 to 8 x 8). Practise regularly to memorise.

The three facts and six facts

Build up the three additional three facts (3 x 6, 3 x 7, 3 x 9) and add to the table.

Double these to get the sixes or use other known facts (e.g. six fours is five fours and four more). Five new facts to learn and their partners give you ten more.

The nine facts

Build on the threes and the sixes using number partitions to add the additional two nine facts and their partners.

Although most are known, revisit the nines to link them to 10 – 1 so that children see that 9 x 7 is ten sevens take seven.

Initially, allow the children time to do the calculation using mental arithmetic strategies and gradually help them memorise for speedy recall.

The seven facts

The seven facts are all known by now we hope!

This is not the only possible sequence. It is a sequence that I follow from First Steps Maths, an excellent resource that is in use in many schools throughout Australia.

It is a sequence and strategy that I have used successfully in a number of schools with different age levels.

The important thing is to assist children in developing mental strategies rather than rote memory to learn the facts.

I hope this helps!